Přírodovědecká fakulta Masarykovy univerzity
Bc. Monika Stančíková
Základní kombinatorická pravidla
Kombinatorická pravidla, ačkoli jsou jen dvě, nám vystačí k řešení většiny kombinatorických úloh. Jestliže jste o nich ještě nikdy neslyšeli, jistě jste je někdy ve svém životě použili.
Zřejmě se vám obě pravidla budou zdát jako samozřejmá, ovšem to jim neubírá na významu, obě budeme hojně používat ve všech kapitolách této učebnice.
PRAVIDLO SOUČTU
Lehký příklad na objasnění definice
Ve škole jsou dvě první třídy: 1. A a 1. B. Do třídy 1. A chodí 15 žáků, do třídy 1. B chodí 18 žáků.
Kolik je na škole prváků?
Řešení: (skrýt text)
Tyto 2 množiny žáků (třídy) jsou konečné (počet žáků je konečný) a jsou disjunktní (žádný žák nemůže zároveň chodit do 1. A a do 1. B).
Celkově v 1. A a v 1. B je dohromady 15+18=33 žáků.
PRAVIDLO SOUČINU
Příklad 1 - Zvířata
Adam má 3 zvířata - pštrosa, býka a ovci. Rozhodl se, že 2 ze svých zvířat dá svým kamarádům. Jedno Honzovi a druhé Zbyňkovi.
Kolik má možností, jak zvířata rozdělit mezi Honzu a Zbyňka?
Řešení: (skrýt text)
Ze 3 zvířat máme vybrat jedno pro Honzu a poté ze zbylých 2 zvířat jedno pro Zbyňka:
Přepis řešení:
Adam chce dát 1 zvíře Honzovi(H) a 1 zvíře Zbyňkovi(Z):
H Z → _ _
Pro Honzu vybírá 1 zvíře ze 3. Má tedy 3 různé možnosti, jak ho obdarovat:
3 _
Potom, co už 1 zvíře dal Honzovi, pro Zbyňka zbývají jen 2 možnosti, jak jej obdarovat:
3 2
Celkem je možností: $3 \cdot 2 = 6$.

Příklad 2 - Oblečení
Bára má 3 různá trička a 5 různých sukní.
Kolika způsoby si může vzít tričko a sukni, aby pokaždé vypadala jinak?
Řešení: (skrýt text)
Počítáme počet možností, jak si Bára může vybrat 1 tričko(T) a k tomu 1 sukni(S):
T S → _ _
Bára má 3 různé možnosti, jak si vybrat tričko:
3 _
Potom, co si vybrala tričko, má 5 možností, jak si vybrat sukni:
3 5
Celkem má Bára $ 3 \cdot 5 = 15$ různých způsobů, jak se obléct.

Příklad 3 - Čísla
Určete počet všech trojciferných přirozených čísel, v jejichž dekadickém zápisu se každá číslice vyskytuje nejvýše jednou.
Řešení: (skrýt text)
Počet různých číslic je 10, jsou to: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Pro vytvoření trojciferného čísla, potřebujeme 3 číslice → _ _ _
Na první cifře nemůže být číslice 0, proto máme 9 různých čísel, které na ni můžeme umístit:
9 _ _
Na druhou cifru už můžeme použít i číslici 0, proto máme 10 možných číslic. Ale nesmíme použít tu číslici, která je na první cifře (ze zadání se číslice nesmí opakovat), tedy možností je 10-1=9:
9 9 _
Pro třetí cifru ze všech možných číslic odečítáme dvě, které jsme použili pro první a druhou cifru, dostáváme 8 různých číslic:
9 9 8
Celkem takových čísel je: $ 9 \cdot 9 \cdot 8 = 648$.
Příklady na procvičení
Příklad 1
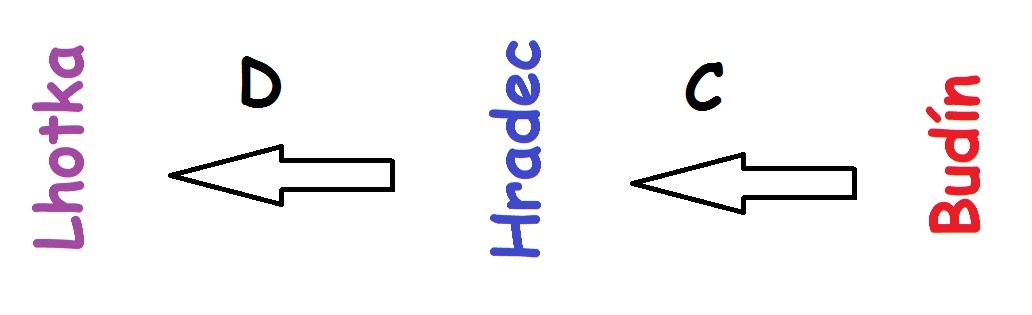
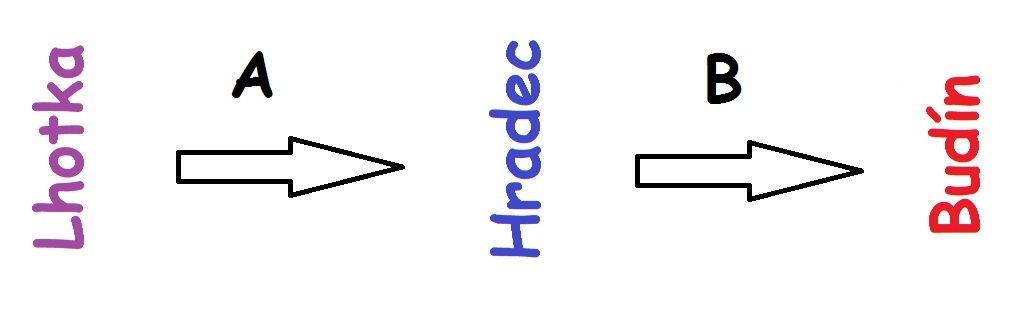
Ze Lhotky do Hradce vedou 3 různé cesty, z Hradce do Budína vedou 4 různé cesty. Určete počet způsobů, jimiž lze vybrat trasu:
- ze Lhotky přes Hradec do Budína a zpět.
- ze Lhotky přes Hradec do Budína a zpět tak, že žádná cesta není použita dvakrát.
- ze Lhotky přes Hradec do Budína a zpět tak, že cesta ze Lhotky do Hradce a z Hradce do Lhotky je ta samá, z Hradce do Budína a zpátky je různá.
Řešení:(zobrazit text)
Příklad 2

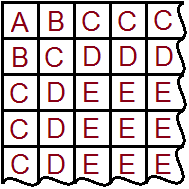
Čtverec o straně délky 4 cm je rozdělen rovnoběžkami se stranami na 16 stejných čtverců.
Určete, kolik je v daném obrazci čtverců?
Řešení:(zobrazit text)
Příklad 3
Biatlonistka Katka má 5 zlatých, 3 stříbrné a 6 bronzových medailí, každou z jiné soutěže.
Chtěla by si některé ze svých medailí pověsit na poličku, která má přesně 5 háčků na pověšení.
Kolik různých možností Katka má, aby si medaile rozvěsila tak, aby na prvním háčku byla jedna ze zlatých medailí, na druhém jedna ze stříbrných, na třetím jedna z bronzových a na posledních dvou libovolná medaile?
Řešení:(zobrazit text)
Příklad 4
Určete celkový počet tahů koně na šachovnici 8x8.
Řešení:(zobrazit text)
Příklad 5
Kolika způsoby lze vybrat na šachovnici 8x8 jedno bílé a jedno černé pole?
Kolika způsoby to lze učinit, nesmějí-li vybraná pole ležet ve stejném řádku ani ve stejném sloupci?
Řešení:(zobrazit text)
Příklad 6

Kolika způsoby lze z úplného souboru domina (28 kostek) vybrat dvě tak, abychom je mohli přiložit k sobě? Tzn., aby se nějaký počet ok vyskytoval zároveň na obou kostkách?
Řešení:(zobrazit text)
Příklad 7
Určete počet všech možných tanečních párů z 15 chlapců a 10 děvčat.
Řešení:(zobrazit text)
Příklad 8
V košíku je 12 jablek a 10 hrušek. Petr si má z něho vybrat jedno ovoce tak, aby Věra, která si po něm vybere jedno jablko a jednu hrušku, měla co největší možnost výběru. Jaké ovoce si má Petr vybrat?
Řešení:(zobrazit text)
Příklad 9
Ve třídě 5. A chodí 14 žáků na němčinu a 13 na francouzštinu. Každý žák navštěvuje právě jeden z uvedených předmětů. Kolika způsoby lze vybrat dvojici na týdenní službu tak, aby měl službu jeden žák z němčiny a jeden žák z francouzštiny?
Kolik let by žáci museli chodit do školy, aby se všechny tyto dvojice vystřídaly? (Počítejte, že školní rok má 33 vyučovacích týdnů.)
Řešení:(zobrazit text)
Příklad 10
Určete počet čtyřciferných čísel, které začínají cifrou 1 a nekončí cifrou 2, nebo končí cifrou 2 a nezačínají cifrou 1.
Řešení:(zobrazit text)
ÚMS, Přírodovědecká fakulta, Masarykova univerzita |
Návrat na úvodní stránku webu, přístupnost |
| Servisní středisko pro e-learning na MU
| Fakulta informatiky Masarykovy univerzity, 2013